正弦函數(shù)的單調性
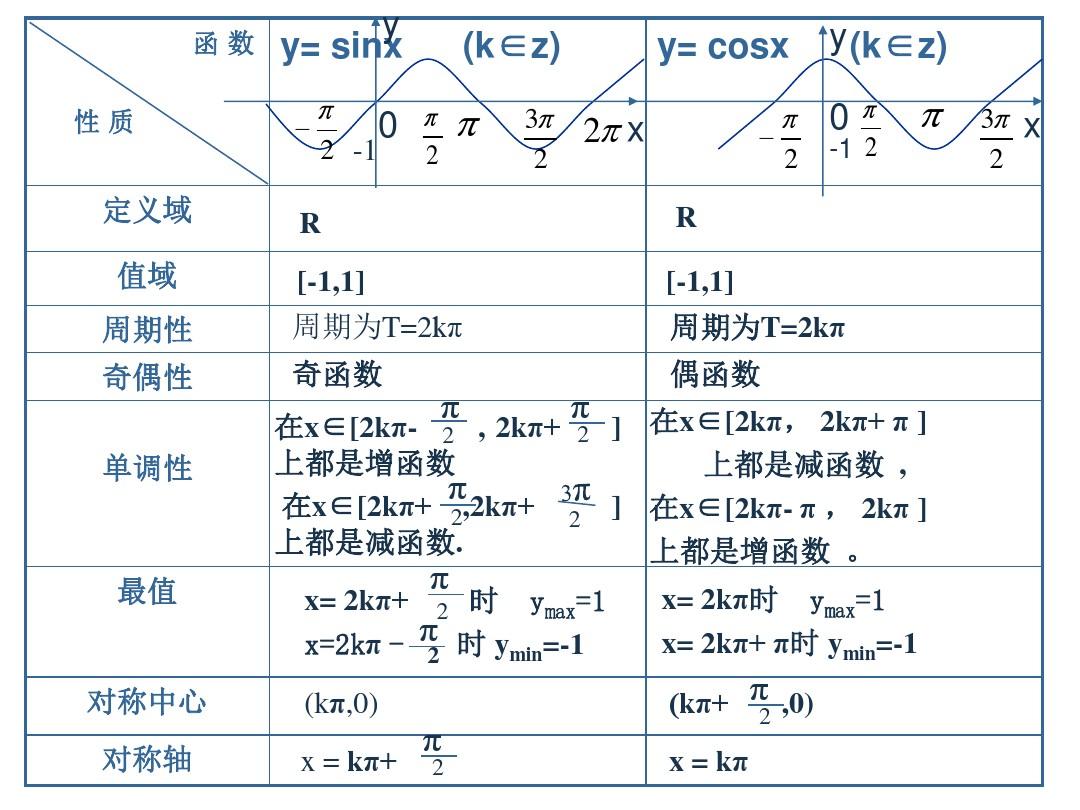
正弦函數(shù) \( y = \sin(x) \) 是一個周期函數(shù),其周期為 \( 2\pi \)。它的圖像在每個周期內呈現(xiàn)出特定的單調性。
1. 單調遞增區(qū)間:
- 在每個周期內,正弦函數(shù)從 \( -\frac{\pi}{2} \) 到 \( \frac{\pi}{2} \) 之間是單調遞增的。
- 用區(qū)間表示,就是 \( [2k\pi - \frac{\pi}{2}, 2k\pi + \frac{\pi}{2}] \),其中 \( k \) 是任意整數(shù)。
2. 單調遞減區(qū)間:
- 在每個周期內,正弦函數(shù)從 \( \frac{\pi}{2} \) 到 \( \frac{3\pi}{2} \) 之間是單調遞減的。
- 用區(qū)間表示,就是 \( [2k\pi + \frac{\pi}{2}, 2k\pi + \frac{3\pi}{2}] \),其中 \( k \) 是任意整數(shù)。
3. 極值點:
- 正弦函數(shù)在 \( x = k\pi \) 處取得局部極值,其中 \( k \) 是任意整數(shù)。
- 當 \( k \) 為偶數(shù)時,\( x = k\pi \) 是局部最大值點,此時 \( y = \sin(x) = 0 \)。
- 當 \( k \) 為奇數(shù)時,\( x = k\pi \) 是局部最小值點,此時 \( y = \sin(x) = 0 \)。
4. 周期性:
- 正弦函數(shù)在整個實數(shù)域上是周期性的,周期為 \( 2\pi \)。
這些性質可以通過正弦函數(shù)的圖像直觀地理解,也可以通過三角函數(shù)的性質和導數(shù)來分析。正弦函數(shù)的導數(shù) \( y' = \cos(x) \) 可以幫助我們確定函數(shù)的增減性。當 \( \cos(x) > 0 \) 時,正弦函數(shù)遞增;當 \( \cos(x) < 0 \) 時,正弦函數(shù)遞減。
判斷函數(shù)單調性的方法
判斷函數(shù)的單調性通常有以下幾種方法:
1. 定義法:
- 利用函數(shù)單調性的定義:如果對于定義域內的任意兩個數(shù) \( x_1 \) 和 \( x_2 \),當 \( x_1 < x_2 \) 時,都有 \( f(x_1) < f(x_2) \),則函數(shù)是增函數(shù);如果 \( f(x_1) > f(x_2) \),則函數(shù)是減函數(shù)。
2. 導數(shù)法:
- 對函數(shù)求導,得到導函數(shù) \( f'(x) \)。
- 如果在某個區(qū)間內 \( f'(x) > 0 \),則原函數(shù)在這個區(qū)間內是增函數(shù)。
- 如果 \( f'(x) < 0 \),則原函數(shù)在這個區(qū)間內是減函數(shù)。
3. 二階導數(shù)法:
- 對函數(shù)求二階導數(shù) \( f''(x) \)。
- 如果在某個區(qū)間內 \( f''(x) > 0 \),則原函數(shù)在這個區(qū)間內是凸函數(shù),通常意味著是增函數(shù)。
- 如果 \( f''(x) < 0 \),則原函數(shù)在這個區(qū)間內是凹函數(shù),通常意味著是減函數(shù)。
4. 復合函數(shù)的單調性:
- 如果兩個函數(shù) \( f(x) \) 和 \( g(x) \) 都是增函數(shù),那么它們的復合函數(shù) \( f(g(x)) \) 也是增函數(shù)。
- 如果 \( f(x) \) 是增函數(shù),\( g(x) \) 是減函數(shù),那么 \( f(g(x)) \) 是減函數(shù)。
5. 利用函數(shù)的性質:
- 某些特定類型的函數(shù)(如指數(shù)函數(shù)、對數(shù)函數(shù)、冪函數(shù)等)具有已知的單調性,可以直接利用這些性質來判斷。
6. 圖形法:
- 繪制函數(shù)的圖像,觀察函數(shù)值隨自變量增加時的變化趨勢。
7. 特殊值法:
- 選取定義域內的一些特殊值,計算函數(shù)值,通過比較這些值的大小來判斷函數(shù)的單調性。
8. 比較法:
- 比較函數(shù)值與某個已知單調性的函數(shù)值,如果函數(shù)值總是大于或小于這個已知函數(shù)的值,可以判斷單調性。
這些方法可以單獨使用,也可以結合使用,以確定函數(shù)在特定區(qū)間內的單調性。
正弦函數(shù)的周期性是什么
正弦函數(shù) \( y = \sin(x) \) 是一個周期函數(shù),它的周期性意味著函數(shù)在某個區(qū)間內重復其值。對于正弦函數(shù),這個周期是 \( 2\pi \)。這意味著,當 \( x \) 的值增加 \( 2\pi \) 的整數(shù)倍時,函數(shù)的值會重復出現(xiàn)。
具體來說,正弦函數(shù)的周期性可以通過以下等式表達:
\[ \sin(x + 2\pi n) = \sin(x) \]
其中 \( n \) 是任意整數(shù)。
這個性質使得正弦函數(shù)在數(shù)學、物理學和工程學等領域有著廣泛的應用,例如在描述波動和振動現(xiàn)象時。

 微信掃一掃打賞
微信掃一掃打賞